If you’ve fallen far enough down the Wordle rabbit hole you may have heard of Quordle, a version of Wordle where you solve four words at once. If you’re looking for more of a challenge, Britannica has you covered with Octordle, where you solve eight words at once. And of course any Wordler worth their salt should be able to handle sixteen words, like in Sedecordle. And no, it doesn’t stop there:

Sexaginta-quattuordle isn’t real, it can’t hurt yo–

One logical extreme of this trend would be to take the list of 2315 valid secret words to create duomilia-trecenti-quindecordle, where each day the puzzle is a different permutation of those 2315¹ words. Despite how chaotic the user interface would need to be, this variant wouldn’t be much of a challenge. Since the same guess is applied to all 2315 words every turn, entering each of the 2315 secret words in any order will always solve it with a perfect score of 2315 guesses.

But what if you could enter different guesses for each of the 2315 secrets each turn? I call this Hyper Wordle since it can be viewed as an exponentially larger version of normal Wordle:

Normal Wordle	Hyper Wordle
Secrets are chosen from the \(2315\) possible 5-letter secret words.	2315 secrets are chosen from the \(2315!\) possible permutations of 5-letter secret words.
Each turn a guess is chosen from \(12972\) possible 5-letter words.2	Each turn 2315 guesses are chosen from \(12972^{2315}\) possible tuples of 5-letter words.
Feedback is given in the form of \(5\) colored squares.	Feedback is given in the form of \(5 \times 2315 = 11575\) colored squares.
Your score is the number of 5-letter guesses needed to identify the secret.	Your score is the total number of 5-letter guesses needed to identify each word in the secret permutation.

Believe it or not, this is a real Wordle variant I ran into back in 2022 as part of a competition to see who could write the best Wordle solving program. The intended way to play was to treat each secret word in the permutation as its own game, effectively playing 2315 independent games of Wordle. For example, if you used the optimal³ Wordle strategy starting with the word SALET (average score of ≈3.4212 guesses) against every secret in the permutation, submissions would always score exactly \(3.4212 \times 2315 = 7920\) since every potential secret word always appears exactly once.

7920 is by no means a bad score, but can we do better? For example, can we take advantage of the fact that the secrets are permuted without replacement to gain extra information? After all, even if SALET is optimal for Wordle, it isn’t necessarily optimal for Hyper Wordle.

Wacky Trick Leaks Extra State

Before we try to solve a permutation of 2315 words, let’s consider a simpler scenario where we’re solving a permutation of six secret words in parallel: FIRST, DEUCE, THIRD, FORTH, FIFTH, SIXTH. Let’s take a look at a strategy where LEAKS is our starting word:

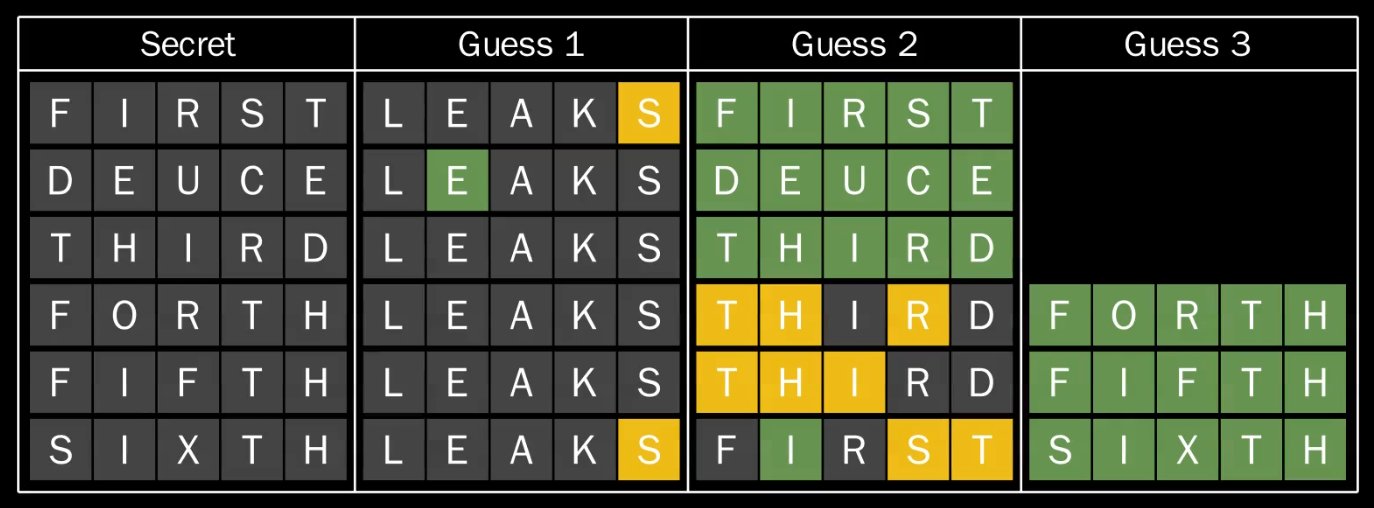
This strategy treats each secret independently, meaning our guess for each word is based solely on feedback we’ve received for the word so far. While we show the secret words in order here, since the strategy treats each secret independently it always requires a total of 15 guesses to solve all the words regardless of how they’re permuted. Next, consider a strategy with MAJOR as our starting word:

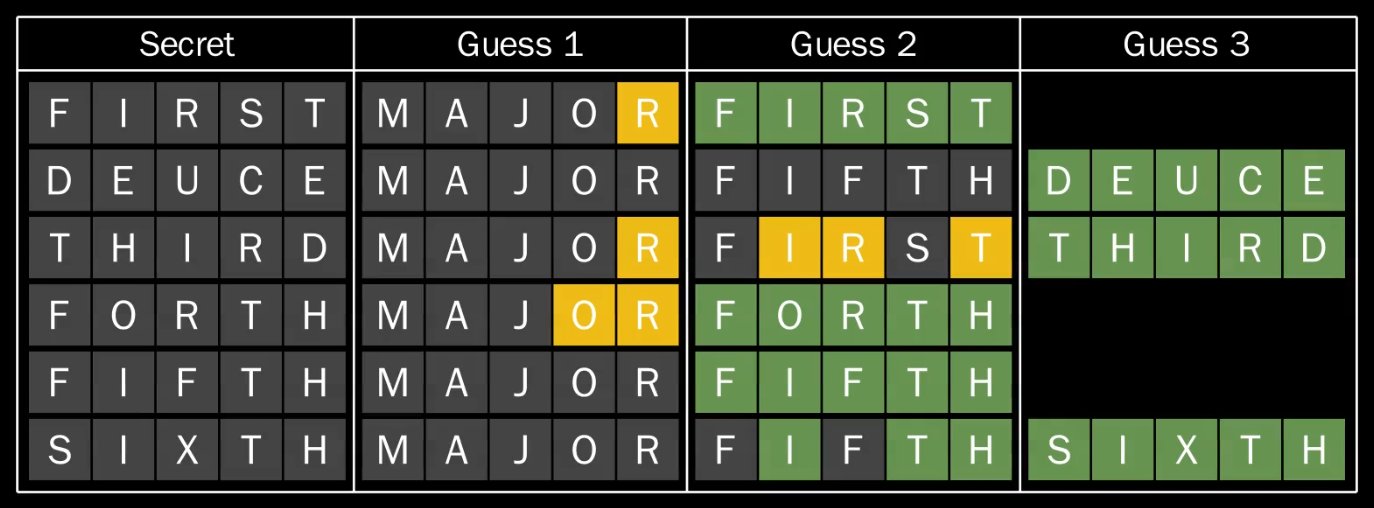
Again, this strategy requires 15 guesses to solve any permutation of the 6 chosen secret words. Neither the MAJOR strategy nor LEAKS strategy are particularly impressive on their own. Let’s try to solve an unknown permutation of our secret words while mixing the two starting words, with MAJOR for the first three positions and LEAKS for the last three:

To put you in the mindset of the puzzle, the actual value of each secret word is kept, well, secret. The only information you have is that each of the six secret words appears only once, but can be in any order. The possibilities column lists the possible secret words which can be in a position based on the feedback from guess 1, using 1, 2, 3, 4, 5, and 6 as shorthand for FIRST, DEUCE, THIRD, FORTH, FIFTH, and SIXTH respectively.

Before we make any more guesses, is there anything we can do to narrow down the values in the possibilities column? Looking closely, we already know the position of 2: it must be in the fourth position since it’s the only secret which matches that feedback pattern for LEAKS. This allows us to remove 2 from the lists of possibilities in the first two positions:

Now that we’ve removed 2 as a possibility in the first and second positions, we see the first position must be either 5 or 6. Consider the following two scenarios:

• If 5 is in the first position, 6 must be in the second position since there would be no other option that could go there.
• If 6 is in the first position, 5 must be in the second position since there would be no other option that could go there.

In Sudoku⁴ puzzles these are known as Naked Candidates. While we don’t know which of the two scenarios we’re in yet, in every scenario 5 and 6 must be in the first two positions, allowing us to rule them out from any other position:

After this deduction, we know 1 must be in the fifth position since it’s the only viable option. This allows us to remove it from the list of possibilities for the third position.

By the same logic, 3 must be in the third position, and we can remove it from the possibilities for the sixth position.

Finally, we can deduce 4 must be in the sixth position. Initially we only knew the position of 2, however after applying deductions we learn the exact position of four out of the six secrets! If we submit guesses tuned to take advantage of our updated knowledge:

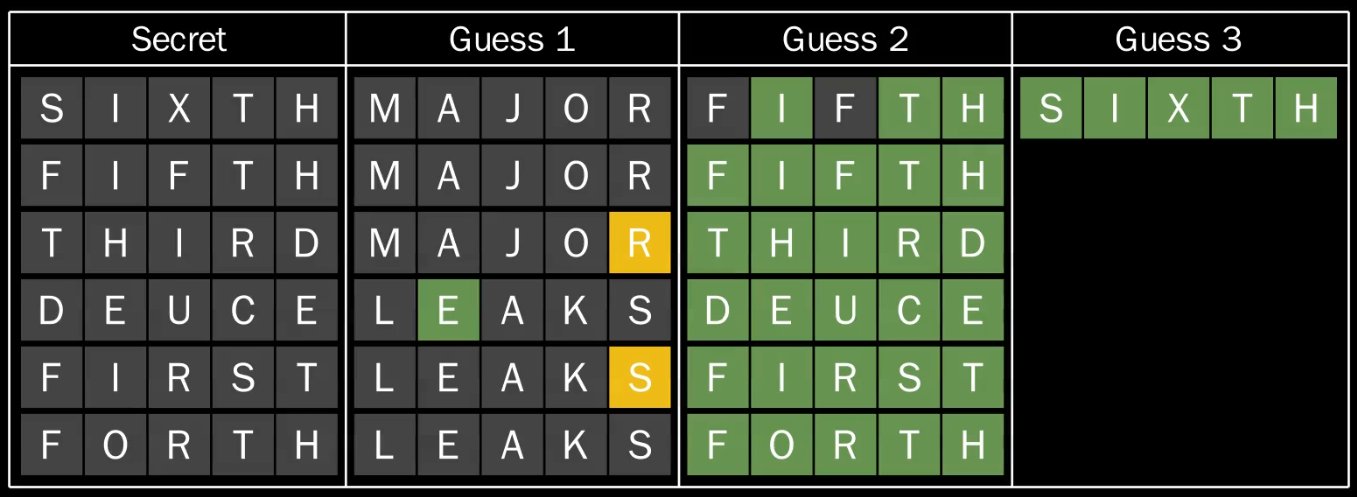
We’re able to solve every word in a total of 13 guesses, an improvement over 15 guesses for both the MAJOR strategy and the LEAKS strategy on their own. Taking a step back, where did this improvement come from? Note that the individual MAJOR and LEAKS strategies each have their own strengths and weaknesses:

• MAJOR always knows the location of FORTH after submitting guess 1, while LEAKS doesn’t find this out until after guess 2.
• LEAKS always knows the location of DEUCE after submitting guess 1, while MAJOR doesn’t find this out until after guess 2.

In the example we worked through above, notice how the first deduction uses information from the LEAKS half of the puzzle to rule out the location of DEUCE (2) in the MAJOR half of the puzzle earlier than it normally could. In other words, LEAKS’ strengths cover for MAJOR’s weaknesses, which in turn gives MAJOR enough information to cover LEAKS’ weaknesses. By exploiting the asymmetry in the strengths and weaknesses of each strategy, we’re able to iteratively refine both strategies to perform better than the sum of their parts!

We can brute force over all \(6! = 720\) possible permutations of our secret words to build up histograms showing how much improvement deduction gives us on average:

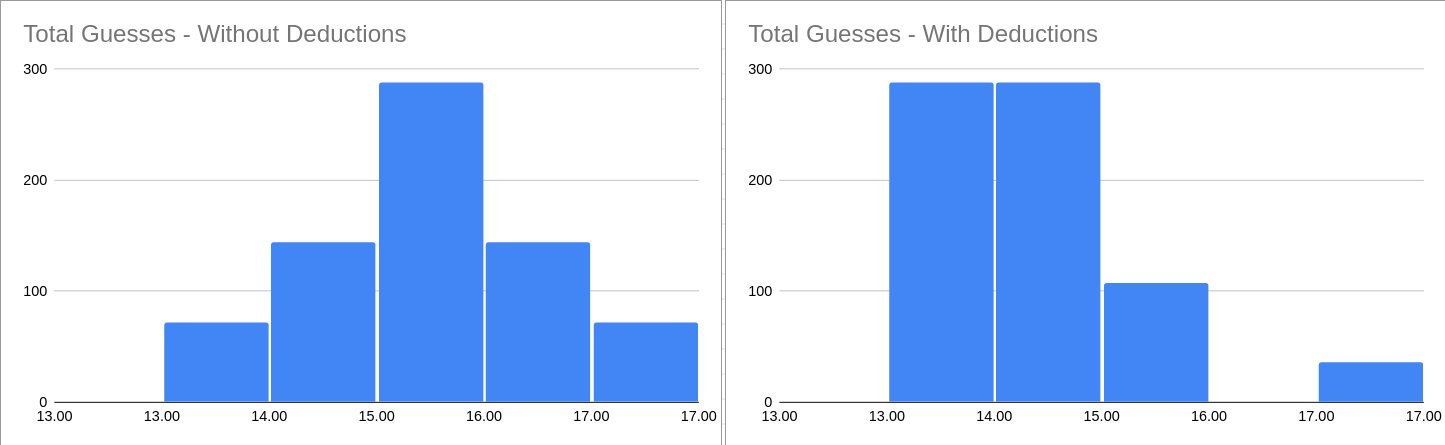
On the left, we have the result of mixing the two strategies without using any deduction tricks. This produces a vaguely Gaussian looking distribution averaging a score of 15, the same as using MAJOR or LEAKS on their own. Note that variance comes from the fact that MAJOR and LEAKS each have their own strengths and weaknesses:

• The score is lower for permutations where secrets MAJOR/LEAKS solve quickly are shuffled into their halves.
• The score is higher for permutations where secrets MAJOR/LEAKS solve slowly are shuffled into their halves.

On the right, we have the result of mixing the two strategies and using deduction tricks to refine our guesses with an average score of 13.9, a 1.1 point improvement!

Widen Scope

Now that we’ve seen this work with permutations of six secret words, let’s see how we do against permutations of the complete list 2315 secret words. We can start off by mixing the best Wordle strategy starting with SALET (score of 7920) with the second best strategy starting with REAST (score of 7923):

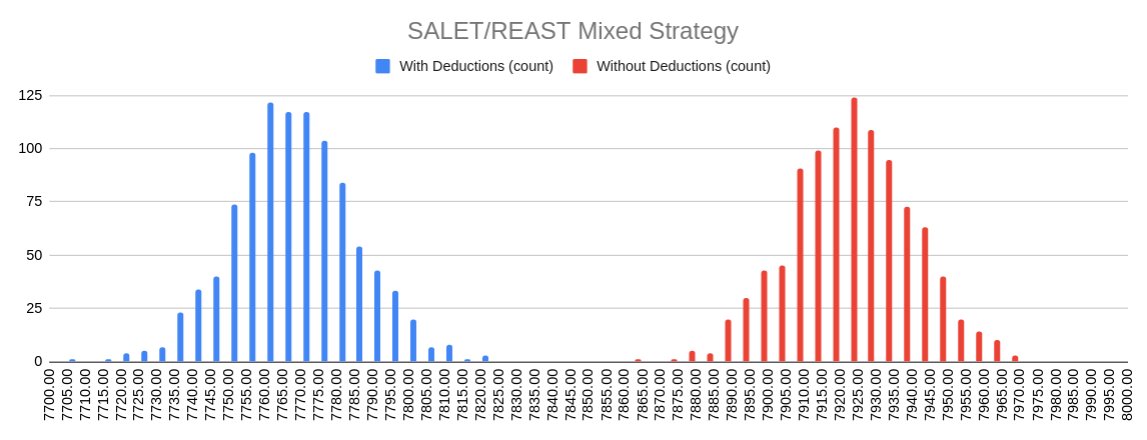
The values on the right are show the score distribution of the SALET/REAST mixed strategy on 1000 random permutations of the 2315 secret words without any deduction. On the left we have the results on the same 1000 permutations after eliminating possible states via deduction each turn and refining our guessing strategy accordingly. Deduction takes our average score from ≈7921.5 to ≈7768.8, a 150 point improvement!

SALET and REAST were chosen since they’re the top two Wordle strategies, but what about mixing other strategies? During the competition, the best combination of strategies I found was by assigning 10% of the permutation to each of the top 10 Wordle starting words: SALET, REAST, CRATE, TRACE, SLATE, CRANE, CARLE, SLANE, CARTE, and TORSE. Plotting this against the previous two histograms:

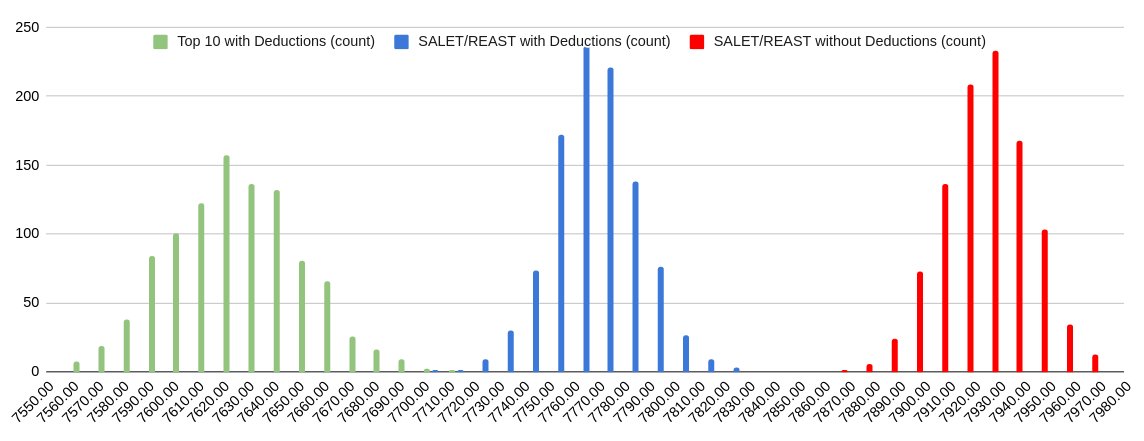
The top 10 mix with deduction is shown in green with an average score of ≈7628.0, an additional 130 point improvement over the SALET/REAST deduction strategy! Trying to mix in more words (e.g. top 20) seems to have diminishing returns since introducing less efficient starting words drags the expected score without deductions up. The top 10 mixed strategy is what I ultimately used in the competition mentioned earlier, winning with a score of 7574 – a ≈4.4% improvement over the optimal Wordle strategy by itself!

Bonus Trick

While proofreading the diagrams for the smaller 6-secret word case, I realized there’s a second deduction strategy commonly known as Hidden Candidates which is “dual” to the Naked Candidates trick. Going back to the diagram:

Given the feedback from guess 1, notice there’s only 1 possible location where 4 can go, meaning 4 must be in the 6th position:

After updating the possibilities in the 6th position, notice that the only valid location for 3 is in the third position, meaning it must be there:

And so on. After generalizing this trick for subsets of N words with only N possible locations, we can incorporate it into the top 10 mixed strategy to squeeze out some extra performance:

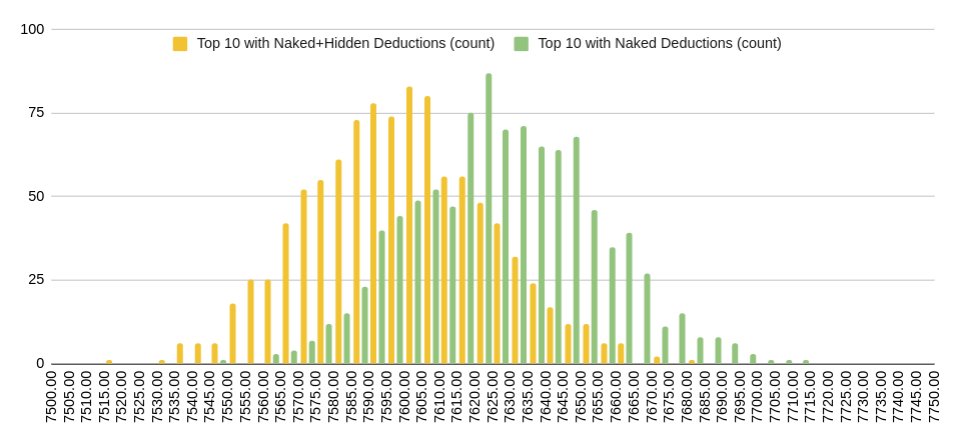
This takes our average from ≈7628.0 to ≈7598.3, averaging a 320 point improvement over the best Wordle strategy’s score of 7920. To put this into perspective, this is the same as the amount improvement between the best Wordle strategy and the 3334th best Wordle strategy!

Final Words

If you want to tinker with ideas, I generated all the data for the strategy histograms in this post using this very adhoc Rust code. Some interesting open questions are:

• What’s the best mix of two starting words (i.e. lowest average score)? Intuitively, some starting words might “synergize” with each other better than others if the structure of their decision trees tend to lead to more deductions.
• My winning strategy only behaves non-deterministically on the first turn, when we randomly use 10 different guesses despite every word having identical feedback at that point (i.e. no feedback). Can we get further improvements by behaving non-deterministically on later turns?
• The deduction strategy only removes words from the possibility pool when we’re certain they must be somewhere else. Is there a way to “fuzzily” refine our possibilities to values other than 0, e.g. “this word is likely to be in position A, so it’s less likely to be in position B”?
• In the version of Hyper Wordle played in this writeup, each batch of 2315 guesses can contain duplicates. What do strategies look like if we don’t allow duplicates?
• Are there any other games/scenarios where combining multiple suboptimal strategies outcompetes a strategy which would normally be stronger?
• Should I find less convoluted things to do with my free time?

If you enjoyed reading this, this entire writeup was actually much longer before I broke it into three standalone parts. Excluding the one you’re reading right now, the other two are:

• The Sixteen Bottles of Wine Riddle – I thought of this riddle while trying to think of a simpler version Hyper Wordle to use as a toy example to introduce some concepts. Despite trying to make it as simple and symmetric as possible, it still ended up having a surprising amount of depth!
• Writing Wordle bots for fun and profit – This gives some context on some of the other stages of the Wordle strategy competition, which I also happened to win. No novel discoveries to share there, but it’s a fun story anyway if you’re into Wordle.

Anyway, thanks for reading!

---